二进制与十进制的相互转换和实现

数学中的数制

• 数制：数制也称为“计数制”，是用一组固定的符号和统一的规则来表示数值的方法。任何一个数制都包含两个基本要素：基数和位权。
• 数位：指一个数中每一个数字所占的位置。
• 基数：指在某种进位计数制中，数位上所能使用的数字符号的个数。
• 位权：是一个数学名词，指数制中每一固定位置对应的单位值。如十进制数的特点是逢十进一。

数制的计算

1. 十进制数的特点是逢十进一

2. 二进制的特点是逢二进一

3. 十六进制的特点是逢十六进一

十进制转二进制

正整数转二进制

方式：将一个十进制数除以2，得到的商再除以2，以此类推直到商等于1或者0为止，倒序取得的余数即为二进制数的结果。只需记住要点：除二取余，倒序排列，高位补零。

由于计算机内部表示数的字节单位都是定长的，以2的幂次展开，或者8位，或者16位，或者32位等等。于是，一个二进制数用计算机表示时，位数不足2的幂次时，高位上要补足若干个0。本文都以8位为例。

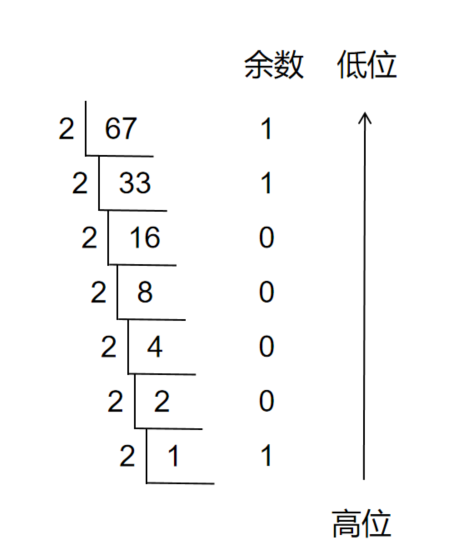
从图中可知，十进制数67的二进制数为01000011（高位不足需要补零）。

负数转二进制

方法：先是将对应的正整数转换成二进制后，对二进制取反，然后对结果再加一。以67为例，即-67经过转换后最终转化为二进制数：10111101。

1. 67的二进制为：01000011
2. 对01000011取反得：10111100
3. 对10111100加一得：10111101

小数转二进制

方法：乘2取整法，即将小数部分乘以2，然后取整数部分，剩下的小数部分继续乘以2，然后取整数部分，剩下的小数部分又乘以2，一直取到小数部分为零为止。如果永远不能为零，就同十进制数的四舍五入一样，按照要求保留多少位小数时，就根据后面一位是0还是1，取舍，如果是零，舍掉，如果是1，向前入一位。换句话说就是0舍1入。读数要从前面的整数读到后面的整数，下面以0.125转二进制为例：

0.125的二进制数为0.001，换算步骤：

1. ，整数部分为0，小数部分为0.25；
2. ，整数部分为0，小数部分为0.5；
3. ，整数部分为1，小数部分为0，此时不需要计算了；
4. 读数，从步骤1的整数部分读起，读到最后一步的整数部分，得0.001。

假设整数部分不为0的小数，换算也是类似，先将整数部分换算成二进制，然后将小数部分换算二进制。例如67.125的二进制为：01000011.001。

二进制转十进制

正整数二进制转十进制

方法：从二进制的右边第一个数开始，每一个数乘以2的n次方，n从0开始，每次递增1。然后得出来的每个数相加即是十进制数。

以二进制01000011为例：

负数二进制转十进制

方法：负数二进制的最高位为1。先将二进制取反，然后加1得到负数绝对值的二进制，转换成十进制后加上负数符号-即可。

以二进制10111101为例：

1. 对10111101取反得01000010；

2. 对01000010加1得01000011；

3. 将01000011转为十进制，得到绝对值67；

4. 加上负数符号得到结果：-67。

小数二进制转十进制

方法：整数部分按照整数二进制转十进制的方法转换；小数部分需要从小数点开始（从1开始），第1为乘以，第n位乘，然后相加。

以二进制01000011.001为例：

1. 整数部分01000011转为十进制得：67；

2. 小数部分.001转二进制得：0.125；

3. 最后取得结果为：67.125。

程序实现

十进制转二进制

方式1

// DecimalToBinaryBigEnd 十进制转二进制
// 低位在前，高位在后。如果想要高位在前，翻转一下数组即可
func DecimalToBinaryBigEnd(number int) [32]int {
	bits := [32]int{}

	k := 0
	for number != 0 {
		bits[k] = number & 1
		number >>= 1
		k++
	}

	return bits
}

// 单元测试
func TestDecimalToBinaryBigEnd(t *testing.T) {
	type args struct {
		number int
	}
	tests := []struct {
		name string
		args args
		want [32]int
	}{
		{
			name: "67",
			args: args{
				number: 67,
			},
            // 注意：这里的实现是低位在前，高位在后
			want: [32]int{1, 1, 0, 0, 0, 0, 1},
		},
	}
	for _, tt := range tests {
		t.Run(tt.name, func(t *testing.T) {
			if got := DecimalToBinaryBigEnd(tt.args.number); !reflect.DeepEqual(got, tt.want) {
				t.Errorf("DecimalToBinary() = %v, want %v", got, tt.want)
			}
		})
	}
}

方式2

// DecimalToBinaryBigEnd 十进制转二进制
// 低位在前，高位在后
func DecimalToBinaryBigEnd(number int) [32]int {
	bits := [32]int{}

	mask := 1
	for i := 0; i < 32; i++ {
		if number&mask != 0 {
			bits[i] = 1
		}
		mask <<= 1
	}

	return bits
}

二进制转十进制

// BinaryToDecimalBigEnd 二级制转化成十进制
// 低位在前，高位在后
func BinaryToDecimalBigEnd(bits [32]int) int {
	number := 0
	mask := 1 // 2^0

	for i := 0; i < 32; i++ {
		number += bits[i] * mask
		mask <<= 1
	}

	return number
}

// 单元测试

func TestBinaryToDecimalBigEnd(t *testing.T) {
	type args struct {
		bits [32]int
	}
	tests := []struct {
		name string
		args args
		want int
	}{
		{
			name: "67",
			args: args{
                // 注意：这里的实现是低位在前，高位在后
				bits: [32]int{1, 1, 0, 0, 0, 0, 1},
			},
			want: 67,
		},
	}
	for _, tt := range tests {
		t.Run(tt.name, func(t *testing.T) {
			if got := BinaryToDecimalBigEnd(tt.args.bits); got != tt.want {
				t.Errorf("BinaryToDecimal() = %v, want %v", got, tt.want)
			}
		})
	}
}